总结一些常用的算法思路和模板
搜索#
1. 二分查找#
int binary_search(vector<int>& nums,int target)
{
int left = 0;
int right = nums.size() - 1;
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] > target){
right = mid - 1;
}else if(nums[mid] < target){
left = mid + 1;
}else{
return mid;
}
}
return -1;
};
2. 双指针#
// 时间复杂度:O(n)
// 空间复杂度:O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (val != nums[fastIndex]) {
nums[slowIndex++] = nums[fastIndex];
}
}
return slowIndex;
}
};
排序#
1. 排序-选择排序#
void selectionSort(vector<int>& nums) {
int n = nums.size();
for(int i = 0; i < n-1; i++){
int k = i;
for(int j = i+1; j < n; j++){
if(nums[j] < nums[k]){
k = j;
}
}
swap(nums[i],nums[k]);
}
}
2. 排序-冒泡排序#
void bubbleSort(vector<int>& nums) {
int n = nums.size();
for(int i = n-1; i>0; i--){
for(int j = 0; j < i; j++){
if(nums[j] > nums[j+1]){
swap(nums[j],nums[j+1]);
}
}
}
}
使用Flag标记优化
void bubbleSort(vector<int>& nums) {
int n = nums.size();
for(int i = n-1; i>0; i--){
bool flag = false;
for(int j = 0; j < i; j++){
if(nums[j] > nums[j+1]){
swap(nums[j],nums[j+1]);
flag = true;
}
}
if(!flag) break;
}
}
3. 排序-插入排序#
void insertionSort(vector<int>& nums) {
int n = nums.size();
for(int i = 1; i < n; i++){
int base = nums[i];
int j = i - 1;
while(j >= 0 && nums[j] > base){
nums[j+1] = nums[j];
j--;
}
nums[j+1] = base; //将base插入到合适的位置
}
}
3. 排序-快速排序#
哨兵划分
int partition(vector<int> &nums, int left, int right) {
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums[i], nums[j]); // 交换这两个元素
}
swap(nums[i], nums[left]); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
快速排序
void quick_sort(vector<int> &nums, int left, int right) {
if(left >= right) return;
int pivot = partition(nums, left, right);
quick_sort(nums, left, pivot - 1); // 排序左子数组
quick_sort(nums, pivot + 1, right); // 排序右子数组
}
4. 排序-归并排序#
/* 合并左子数组和右子数组 */
void merge(vector<int> &nums, int left, int mid, int right) {
// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]
// 创建一个临时数组 tmp ,用于存放合并后的结果
vector<int> tmp(right - left + 1);
// 初始化左子数组和右子数组的起始索引
int i = left, j = mid + 1, k = 0;
// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中
while (i <= mid && j <= right) {
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
}
// 将左子数组和右子数组的剩余元素复制到临时数组中
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间
for (k = 0; k < tmp.size(); k++) {
nums[left + k] = tmp[k];
}
}
/* 归并排序 */
void mergeSort(vector<int> &nums, int left, int right) {
// 终止条件
if (left >= right)
return; // 当子数组长度为 1 时终止递归
// 划分阶段
int mid = left + (right - left) / 2; // 计算中点
mergeSort(nums, left, mid); // 递归左子数组
mergeSort(nums, mid + 1, right); // 递归右子数组
// 合并阶段
merge(nums, left, mid, right);
}
5. 排序-堆排序#
/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(vector<int> &nums, int n, int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = 2 * i + 1;
int r = 2 * i + 2;
int ma = i;
if (l < n && nums[l] > nums[ma])
ma = l;
if (r < n && nums[r] > nums[ma])
ma = r;
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma == i) {
break;
}
// 交换两节点
swap(nums[i], nums[ma]);
// 循环向下堆化
i = ma;
}
}
/* 堆排序 */
void heapSort(vector<int> &nums) {
// 建堆操作:堆化除叶节点以外的其他所有节点
for (int i = nums.size() / 2 - 1; i >= 0; --i) {
siftDown(nums, nums.size(), i);
}
// 从堆中提取最大元素,循环 n-1 轮
for (int i = nums.size() - 1; i > 0; --i) {
// 交换根节点与最右叶节点(交换首元素与尾元素)
swap(nums[0], nums[i]);
// 以根节点为起点,从顶至底进行堆化
siftDown(nums, i, 0);
}
}
分治#
分治算法(Divide and Conquer)是一种将一个复杂问题分解为多个相似的子问题来解决的算法设计范式。它通常包括三个步骤:分解、解决和合并。分治算法的核心思想是将问题划分为更小的子问题,递归地解决这些子问题,然后将它们的结果合并起来得到原问题的解。
1. 分治-分治算法模版#
// 分治函数模板
ReturnType divideAndConquer(const vector<int>& input, int left, int right) {
// 1. 递归终止条件
if (left == right) {
// 对于只包含一个元素的情况,直接返回结果
return input[left]; // 举例:最大值/最小值/计数等
}
// 2. 分成左右两部分
int mid = left + (right - left) / 2;
// 3. 递归解决子问题
ReturnType leftResult = divideAndConquer(input, left, mid);
ReturnType rightResult = divideAndConquer(input, mid + 1, right);
// 4. 合并左右结果
ReturnType result = merge(leftResult, rightResult);
return result;
}
// 合并函数示意(可根据题目自定义逻辑)
ReturnType merge(ReturnType left, ReturnType right) {
// 举例:求最大值
return max(left, right);
}
2. 分治-构建树#
class TreeNode {
public:
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
/* 构建二叉树:分治 */
TreeNode *dfs(vector<int> &preorder, unordered_map<int, int> &inorderMap, int i, int l, int r) {
// 子树区间为空时终止
if (r - l < 0)
return NULL;
// 初始化根节点
TreeNode *root = new TreeNode(preorder[i]);
// 查询 m ,从而划分左右子树
int m = inorderMap[preorder[i]];
// 子问题:构建左子树
root->left = dfs(preorder, inorderMap, i + 1, l, m - 1);
// 子问题:构建右子树
root->right = dfs(preorder, inorderMap, i + 1 + m - l, m + 1, r);
// 返回根节点
return root;
}
/* 构建二叉树 */
TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
// 初始化哈希表,存储 inorder 元素到索引的映射
unordered_map<int, int> inorderMap;
for (int i = 0; i < inorder.size(); i++) {
inorderMap[inorder[i]] = i;
}
TreeNode *root = dfs(preorder, inorderMap, 0, 0, inorder.size() - 1);
return root;
}
回溯#
回溯算法(Backtracking)是一种通过尝试所有可能的解来解决问题的算法。它通常用于组合、排列、子集等问题。回溯算法的核心思想是:在每一步选择中,尝试所有可能的选择,并在选择后进行递归搜索;如果发现当前选择不满足条件,则撤销该选择,回到上一步进行其他选择。 尝试与回退
1. 回溯算法模版#
/* 回溯算法框架 */
void backtrack(State *state, vector<Choice *> &choices, vector<State *> &res) {
// 判断是否为解
if (isSolution(state)) {
// 记录解
recordSolution(state, res);
// 不再继续搜索
return;
}
// 遍历所有选择
for (Choice choice : choices) {
// 剪枝:判断选择是否合法
if (isValid(state, choice)) {
// 尝试:做出选择,更新状态
makeChoice(state, choice);
backtrack(state, choices, res);
// 回退:撤销选择,恢复到之前的状态
undoChoice(state, choice);
}
}
}
2. 回溯-全排列问题#
/* 全排列问题 */
void backtrack(vector<int> &state,const vector<int> &choices, vector<vector<int>> &res) {
// 当达到长度时,判断是否为解,并记录
if (state.size() == choices.size()) {
res.push_back(state);
return;
}
// 遍历所有选择
for (int i = 0; i < choices.size(); i++) {
int choice = choices[i];
// 剪枝:判断选择是否合法
if(!selected[i]){
// 尝试:做出选择,更新状态
state.push_back(choice);
selected[i] = true;
// 递归调用,进行下一层的搜索
backtrack(state, choices, res);
// 回退:撤销选择,恢复到之前的状态
state.pop_back();
selected[i] = false;
}
}
}
/* 全排列问题 */
vector<vector<int>> permute(vector<int> &nums) {
vector<vector<int>> res; // 存储结果
vector<int> state; // 当前状态
vector<bool> selected(nums.size(), false); // 记录选择
backtrack(state, nums, res); // 调用回溯函数
return res;
}
3. 子集和问题#
/* 回溯算法:子集和 I */
void backtrack(vector<int> &state, int target, int total, vector<int> &choices, vector<vector<int>> &res) {
// 子集和等于 target 时,记录解
if (total == target) {
res.push_back(state);
return;
}
// 遍历所有选择
for (size_t i = 0; i < choices.size(); i++) {
// 剪枝:若子集和超过 target ,则跳过该选择
if (total + choices[i] > target) {
continue;
}
// 尝试:做出选择,更新元素和 total
state.push_back(choices[i]);
// 进行下一轮选择
backtrack(state, target, total + choices[i], choices, res);
// 回退:撤销选择,恢复到之前的状态
state.pop_back();
}
}
/* 求解子集和 I(包含重复子集) */
vector<vector<int>> subsetSumINaive(vector<int> &nums, int target) {
vector<int> state; // 状态(子集)
int total = 0; // 子集和
vector<vector<int>> res; // 结果列表(子集列表)
backtrack(state, target, total, nums, res);
return res;
}
动态规划#
动态规划(dynamic programming,DP)是一个重要的算法范式,它将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。 记忆化搜索时一种 “从顶至底” 的方法,而动态规划则是一种 “从底至顶” 的方法。
1. 动态规划模版#
- 第一步:思考每轮的决策,定义状态,从而得到
dp表 - 第二步:找出最优子结构,进而推导出状态转移方程
- 第三步:确定边界条件和状态转移顺序
2. 动态规划-走楼梯#
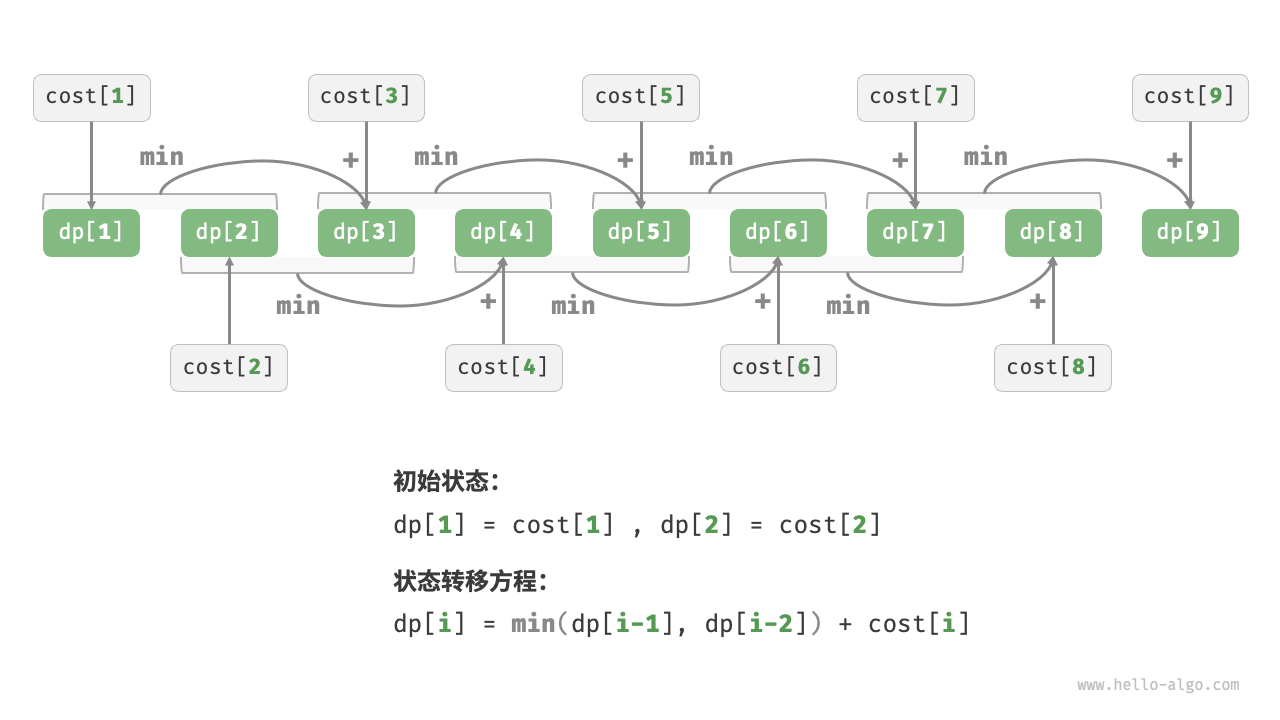
int climbingStairsDP(int n)
{
if(n == 1 || n == 2)
return n;
// 初始化dp表,用于存储子问题的解
vector<int> dp(n + 1, 0);
dp[1] = 1; // 走到第1级台阶的方法数
dp[2] = 2; // 走到第2级台阶的方法数
//状态转移
for(int i=3; i<=n; ++i){
dp[i] = dp[i-1] + dp[i-2]; // 走到第i级台阶的方法数
}
}
如果添加约束,不可以连续跳两个 1 阶
int climbingStairsDP(int n)
{
if(n == 1 || n == 2)
return n;
// 初始化dp表,用于存储子问题的解
vector<vector<int>> dp(n + 1, vector<int>(3,0));
dp[1][1] = 1;
dp[1][2] = 0;
dp[2][1] = 0;
dp[2][2] = 1;
//状态转移
for(int i=3; i<=n; ++i){
dp[i][1] = dp[i - 1][2];
dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
}
return dp[n][1] + dp[n][2];
}
3. 动态规划-01 背包问题#
int knapsackDP(vector<int> &wgt,vector<int> &val,int cap)
{
int n = wgt.size();
// 初始化dp表,用于存储子问题的解
vector<vector<int>> dp(n + 1, vector<int>(cap + 1, 0));
// 状态转移
for(int i=1; i<=n; ++i){
for(int c=1; c<=cap; ++c){
if(c < wgt[i - 1]){
dp[i][c] = dp[i - 1][c]; // 不放入第i个物品
}else{
dp[i][c] = max(dp[i - 1][c],dp[i - 1][c - wgt[i - 1]] + val[i - 1]); // 放入第i个物品
}
}
}
return dp[n][cap]; // 返回最大价值
}
4. 动态规划-零钱兑换#

/* 零钱兑换:动态规划 */
int coinChangeDP(vector<int> &coins, int amt) {
int n = coins.size();
int MAX = amt + 1;
// 初始化 dp 表
vector<vector<int>> dp(n + 1, vector<int>(amt + 1, 0));
// 状态转移:首行首列
for (int a = 1; a <= amt; a++) {
dp[0][a] = MAX;
}
// 状态转移:其余行和列
for (int i = 1; i <= n; i++) {
for (int a = 1; a <= amt; a++) {
if (coins[i - 1] > a) {
// 若超过目标金额,则不选硬币 i
dp[i][a] = dp[i - 1][a];
} else {
// 不选和选硬币 i 这两种方案的较小值
dp[i][a] = min(dp[i - 1][a], dp[i][a - coins[i - 1]] + 1);
}
}
}
return dp[n][amt] != MAX ? dp[n][amt] : -1;
}
贪心#
贪心算法(greedy algorithm)是一种常见的解决优化问题的算法,其基本思想是在问题的每个决策阶段,都选择当前看起来最优的选择,即贪心地做出局部最优的决策,以期获得全局最优解。贪心算法简洁且高效,在许多实际问题中有着广泛的应用。 贪心选择性质与最优子结构
- 贪心选择性质:局部最优解可以推出全局最优解。
- 最优子结构:一个问题的最优解包含其子问题的最优解。
1. 贪心算法模版#
// 通用贪心模板(以排序 + 贪心为核心)
int greedyTemplate(vector<pair<int, int>>& items) {
// 1. 按照某个策略对数据排序
sort(items.begin(), items.end(), [](const pair<int, int>& a, const pair<int, int>& b) {
// 这里定义贪心策略,比如按权重/性价比/结束时间等排序
return a.second < b.second; // 示例:按第二个元素升序排序
});
// 2. 遍历并应用贪心策略
int result = 0;
for (auto& item : items) {
if (/* 当前item满足条件 */) {
// 做出选择
result += item.first; // 示例:累加价值
}
}
return result;
}
2. 贪心-分数背包#
/* 物品 */
class Item {
public:
int w; // 物品重量
int v; // 物品价值
Item(int w, int v) : w(w), v(v) {
}
};
/* 分数背包:贪心 */
double fractionalKnapsack(vector<int> &wgt, vector<int> &val, int cap) {
// 创建物品列表,包含两个属性:重量、价值
vector<Item> items;
for (int i = 0; i < wgt.size(); i++) {
items.push_back(Item(wgt[i], val[i]));
}
// 按照单位价值 item.v / item.w 从高到低进行排序
sort(items.begin(), items.end(), [](Item &a, Item &b) { return (double)a.v / a.w > (double)b.v / b.w; });
// 循环贪心选择
double res = 0;
for (auto &item : items) {
if (item.w <= cap) {
// 若剩余容量充足,则将当前物品整个装进背包
res += item.v;
cap -= item.w;
} else {
// 若剩余容量不足,则将当前物品的一部分装进背包
res += (double)item.v / item.w * cap;
// 已无剩余容量,因此跳出循环
break;
}
}
return res;
}
3. 贪心-Dijkstra 算法#
/* Dijkstra 算法 */
#include<bits/stdc++.h>
#define INF 1000
#define MAX_V 100
using namespace std;
int main()
{
int V,E;
int i,j,m,n;
int cost[MAX_V][MAX_V];
int d[MAX_V];
bool used[MAX_V];
cin>>V>>E;
fill(d,d+V+1,INF);
fill(used,used+V,false);
for(i=0;i<V;i++)
{
for(j=0;j<V;j++)
{
if(i==j) cost[i][j]=0;
else cost[i][j]=INF;
}
}
for(m=0;m<E;m++)
{
cin>>i>>j>>cost[i][j];
cost[j][i]=cost[i][j];
}
cin>>n;
d[n]=0;
//源点
while(true)
{
int v=V;
for(m=0;m<V;m++)
{
if((!used[m])&&(d[m]<d[v])) v=m;
}
if(v==V) break;
used[v]=true;
for(m=0;m<V;m++)
{
d[m]=min(d[m],d[v]+cost[v][m]);
}
}
for(i=0;i<V;i++)
{
cout<<"the shortest distance between "<<n<<" and "<<i<<" is "<<d[i]<<endl;
}
}